ecco un estratto estrapolato da uno dei siti citati:
FRATTALI CREATI CON LA TECNICA L - SYSTEM

L-System è l'acronimo di Lindenmayer-Systems, dal nome di Aristide Lindenmayer (1925-1989), un biologo olandese che per primo sviluppò la tecnica usata per generare questi frattali. Lo scopo di Lindenmayer era di riprodurre in modo virtuale la crescita di svariati tipi di organismi.
L-System non è perciò un tipo di frattale, ma è un metodo che permette di ritrovare i frattali, anche i più noti, come Koch, Sierpinski, alberi etc., che si possono costruire per altra via, purché lineare.
Il metodo adottato da Lindenmayer è molto suggestivo. Si parte da un disegno iniziale (che può essere, ad esempio, un segmento o anche una poligonale). Questo disegno viene riprodotto al computer usando delle regole ben precise:- Regola F
- Avanzare di un segmento di lunghezza assegnata
- Regola f
- Avanzare di un segmento di lunghezza assegnata ma senza lasciare traccia
- Regola +
- Ruotare in senso antiorario di un angolo assegnato
- Regola -
- Ruotare in senso orario di un angolo assegnato
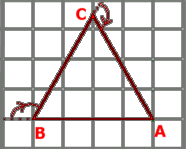
Ad esempio, per costruire il triangolo equilatero in figura, partendo dal vertice A, potremo dare le seguenti istruzioni: vai avanti di un segmento di lunghezza data (arriviamo in B), ruota in senso orario di 120°, vai avanti di un segmento di lunghezza data (arriviamo in C), ruota in senso orario di 120°, vai avanti di un segmento di lunghezza data (torniamo in A). Tradotte queste istruzioni nel nostro linguaggio, potremo scrivere: F-F-F
Ovviamente, affinché la procedura sia effettivamente eseguita da un computer, dovremo dare le istruzioni necessarie per eseguire una rotazione, e dovremo immettere come dati iniziali un valore per l'angolo (in questo caso 120°) e un valore per la lunghezza del segmento (in questo caso 90 pixel).
Fatte queste premesse, vediamo come si possa costruire un frattale.
La costruzione iniziale prende il nome di axiom (assioma). Sulla costruzione iniziale viene poi effettuata una sostituzione secondo una regola assegnata, si ripete il procedimento più volte... ed ecco il frattale!Applichiamo il procedimento per costruire il frattale di Koch:
Dati iniziali:angolo= 60°
lato= numero pixel prescelto (esempio: 900 pixel)
axiom: F
Viene tracciata una linea di lunghezza assegnata
Ripeti:
lato <-- lato/3 Il lato diventa un terzo del precedente
Sostituzione: F <-- F+F--F+F Sostituendo ad ogni F questa stringa,
il segmento
dalla spezzata
(Avanza, ruota di 60° in senso antiorario, avanza, ruota di 60° + 60° = 120° in senso orario, avanza, ruota di 60° in senso antiorario, avanza).
Fino a quando il lato diventa minore di un numero assegnato.
2 comments:
non credo avrà vita lunga questo blog
che detedtive!
perché dici così? cattivo!
In realtà voglio solo organizzarci dentro un portfolio
Posta un commento